Conservation, in terms of physics, can be defined as something that does not change or, specifically, a variable in any condition will be its conservation.
You will find many conserved quantities that help us determine various circumstances and understand their conditions or occurrence. There are three types of conservation in mechanics: conservation of momentum, conservation of energy, and conservation of angular momentum.
Let us first learn about the conservation of momentum. The conservation of momentum always follows the conservation of momentum law which helps us to understand why a specific condition is occurring and how the conservation of momentum works.
Table of Contents
What is momentum?
We need to know what momentum is before we start learning about the conservation of momentum. Momentum is defined as the resultant of the product of velocity and mass. It is a vector quantity, i.e. it has both direction and magnitude. If we take m for mass and v as velocity, the momentum of an object at that point will be P = m. v
The S.I unit of momentum is a kilogram meter per second (kg.m/sec).
Conservation of Momentum?
It is one of the fundamental laws in physics.
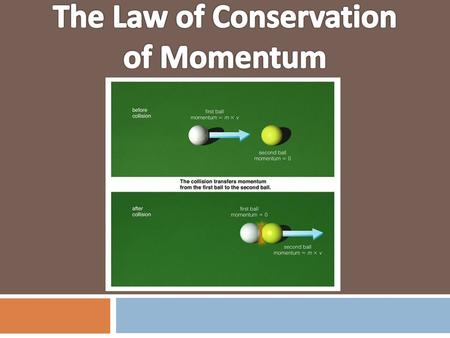
The law states that “for two or more objects in an isolated system acting upon each other, their total momentum remains fixed unless an external force is applied”.
Explanations: if one or more bodies are in an isolated framework or a framework free from any external force that acts on each other, the total momentum of the system of bodies stays the same unless an external force is applied to it.
The total momentum can be calculated with the vector sum of individual momenta of the framework. The total momentum stays along any direction and always remains constant. In any physical process, momentum always stays in equilibrium.
Conservation of Momentum – One Dimension
Conservation of momentum can be easily explained with the help of a one-dimensional collision of bodies. Let us take two objects of the given masses, m1 and m2, moving along a straight line with their velocities u1 and u2, respectively.
The two objects collide with each other, and after the collision, they have a velocity of v1 and v2 and move along the same straight line or the same direction.
The total momentum prior to collision (Pi) = m1u1 + m2u2
The total momentum after collision (Pf) = m1v + m2v2
The total momentum remains constant if no other force acts on it, therefore,
Pi = Pf
M1u1 + m2u2 = m1v1 + m2v2
Deduction of Conservation of Momentum
After the collision of the two objects, if no external force is present, both the objects tend to apply impulse on each other for a short period during the point of contact.
Following Newton’s third law of motion, if the first object exerts an impulsive force on the second object, then equal and opposite impulse force is exerted by the second object on the first one.
During the collision of the two objects, the masses of the two objects m1 and m2 with velocity u1 and u2 before collision and v1 and v2 after collision, the impulse force on the first object applied by the second object is F21 and the impulse force on the second object applied by the first object is F12. with the application of Newton’s Thirds Law,
F21 = F12
If we take t as the time period of contact during the collision, the impulse force F21 will change
F21.t = m1v1 – m1u1
Same as F21, F12 will also have the same changes,
F12 .t = m2v2 – m2u2
From, F21 = -F12
m1v1 – m1u1 = -( m2v2 – m2u2 )
M1u1 + m2u2 = m1v1 – m2v2
This relation shows that the momentum remains constant even during the collision of two objects.
Few Examples of Conservation of Momentum
Here are some of the examples of conservation of momentum of objects in our daily lives. It will help you to understand it in a better way.
The recoil of a gun
If you shoot a bullet from a gun, at first, both the bullet and the gun are still, i.e., the momentum is zero before firing the gun. When the gun is fired, the bullet gains a forward momentum and gets discharged from the gun.
As per the conservation of momentum, the gun gets regressive momentum or backward momentum. Let the mass of the bullet be m and the velocity v, and the mass of the gun be M and the velocity u. Hence, before the firing of the gun, the total momentum is zero. So it is after the firing of the gun.
0 = mv . Mu
u = – mv/M
Here, u is the recoil velocity. The mass of the gun is more than the mass of the bullet, i.e., M >> m. So, the backward velocity of the gun is very less than the forwarding velocity of the bullet u << v
Ballon
As you are blowing into a balloon, the small particles of gases moving inside the balloon quickly collide with one another while crashing with the surface of the balloon. Although the particles are smaller in size and pick up the momentum while colliding, the system’s total momentum remains unchanged and stays the same as before.
Rocket Propulsion
Rockets consist of a gas chamber at one of the ends of the rocket. When the rocket is ready to take off, a huge amount of gas is ejected to help the rocket. Before the gas is ejected, the rocket is in a state of conservation, and the total momentum is zero.
As the gas is ejected from the rocket, the rocket then acquires a recoil velocity and acceleration which acts in the opposite direction. This is due to the conservation of momentum.
Conclusion:
In this article, we learned about the law of conservation of momentum. We learned about the different examples which we can see in our daily lives. The conservation of momentum helps to maintain the equilibrium of the system.
Conservation of momentum is always kept in mind during any scientific experiment. So, it is one of the important parts of physics that will help us understand the law of nature in a better way.
- Guide to Choosing the Best Spy Phone App in 2023 - April 20, 2023
- Playable Ads: Get All the Juice Out of Your Advertising Efforts - April 6, 2023
- 10 Most Notorious Black Hat Hackers in History - March 27, 2023